In the realm of digital electronics and computer science, binary code serves as the foundation for data representation and processing. However, in certain applications, a variation of binary known as Gray code offers unique advantages, particularly in reducing errors during data transmission and processing. This article explores the concept of Gray code, its advantages, applications, and how it differs from traditional binary code.
What is Gray Code?
Gray code, also known as reflected binary code, is a binary numeral system where two successive values differ in only one bit. This property makes Gray code particularly useful in scenarios where a change in more than one bit can lead to errors or unintended consequences.
Example of Gray Code
To understand Gray code better, let’s look at the binary representation of numbers from 0 to 7:
| Decimal | Binary | Gray Code |
|---|---|---|
| 0 | 000 | 000 |
| 1 | 001 | 001 |
| 2 | 010 | 011 |
| 3 | 011 | 010 |
| 4 | 100 | 110 |
| 5 | 101 | 111 |
| 6 | 110 | 101 |
| 7 | 111 | 100 |
As you can see from the table, in Gray code, only one bit changes between successive numbers, which minimizes the chances of errors during transitions.
Advantages of Gray Code
1. Error Reduction
The primary advantage of Gray code lies in its ability to reduce errors, particularly in systems where binary values are read or processed sequentially. When transitioning between two values in binary, multiple bits can change at once, leading to potential misreads. With Gray code, since only one bit changes, the likelihood of misinterpretation is significantly decreased.
2. Simplicity in Mechanical Systems
Gray code is often used in mechanical encoders, which convert the position of a physical object into a binary signal. Since mechanical systems can experience noise and delays, using Gray code minimizes the chance of reading incorrect positions as the encoder moves between states.
3. Efficient Digital Circuit Design
Gray code can simplify the design of digital circuits. Because only one bit changes at a time, the number of transitions is reduced, leading to less power consumption and decreased electromagnetic interference (EMI), which is particularly important in sensitive electronic devices.
Applications of Gray Code
1. Rotary Encoders
Gray code is extensively used in rotary encoders, which are devices that convert the angular position of a shaft into a digital signal. By using Gray code, rotary encoders can provide accurate position readings even in the presence of noise and signal degradation.
2. Digital Communication
In digital communication systems, Gray code can be employed in error detection schemes. When transmitting data, if two successive code words differ by only one bit, the chances of errors occurring during transmission are minimized.
3. Quantum Computing
As quantum computing continues to evolve, Gray code is being explored for use in quantum error correction schemes. Its ability to minimize bit changes during data processing can help enhance the reliability of quantum operations.
4. Analog-to-Digital Converters (ADCs)
Gray code is also utilized in some types of analog-to-digital converters to reduce the complexity of conversion. Since only one bit changes at a time, Gray code can help streamline the conversion process and improve overall efficiency.
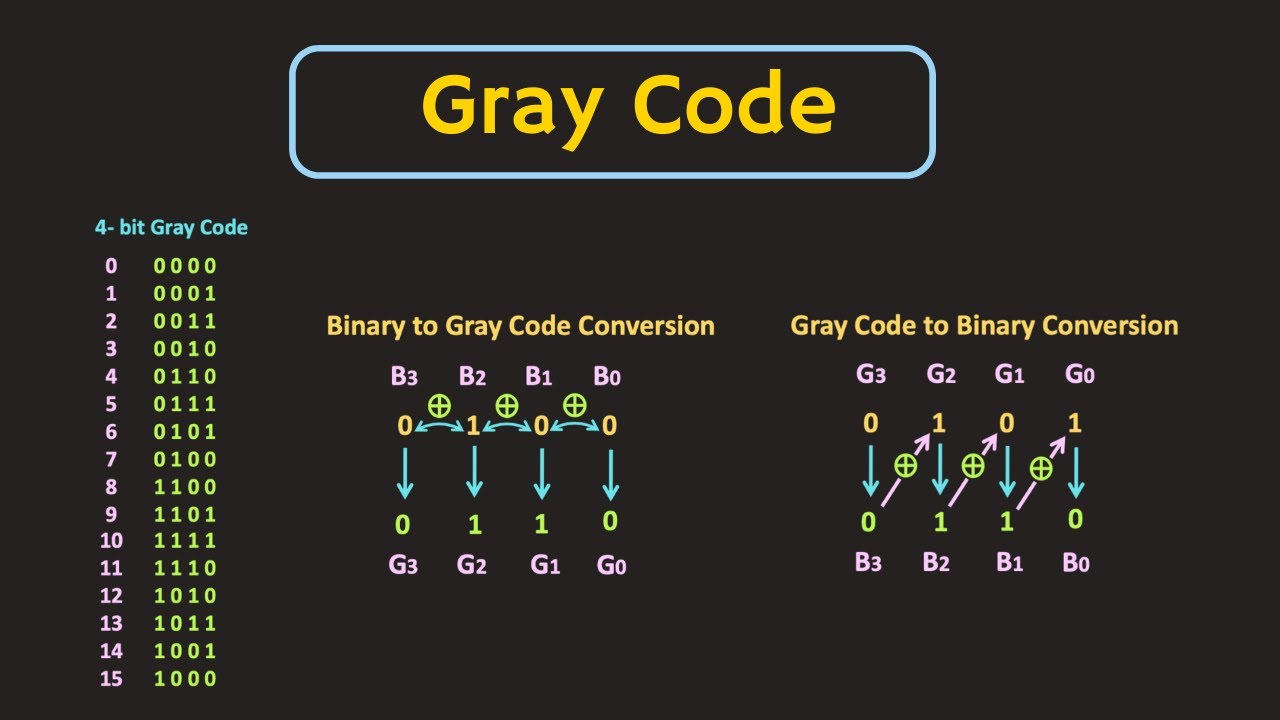
Converting Between Binary and Gray Code
The conversion between binary and Gray code is straightforward. To convert a binary number to Gray code, follow these steps:
- The most significant bit (MSB) of the Gray code is the same as the MSB of the binary code.
- For each subsequent bit, perform an XOR operation between the current bit and the previous bit of the binary code.
Example Conversion: Binary to Gray Code
Let’s convert the binary number 1011 to Gray code:
- The MSB remains the same:
1 - Perform XOR for the remaining bits:
1 XOR 0 = 10 XOR 1 = 11 XOR 1 = 0
So, the Gray code equivalent of binary 1011 is 1110.
Gray Code to Binary Conversion
To convert from Gray code back to binary, the following steps are used:
- The MSB of the binary code is the same as the MSB of the Gray code.
- For each subsequent bit, perform an XOR operation between the current Gray code bit and the previous bit of the binary code.
Example Conversion: Gray Code to Binary
Let’s convert the Gray code 1110 back to binary:
- The MSB remains the same:
1 - Perform XOR for the remaining bits:
1 XOR 1 = 00 XOR 1 = 11 XOR 0 = 1
So, the binary equivalent of Gray code 1110 is 1011.
Conclusion
Gray code offers a valuable alternative to traditional binary code, particularly in applications where error reduction and reliability are paramount. Its unique property of changing only one bit at a time makes it suitable for mechanical systems, digital communication, and various electronic devices. As technology continues to advance, understanding and utilizing Gray code will remain essential for ensuring accuracy and efficiency in a wide range of applications.